Il n'est pas indifférent à une anthropogénie d'insister sur le destin de la flèche à travers la mathématique et son écriture.

Au départ, il s'agit d'un outil, pointe de masse ou arme de chasse, mais comportant implicitement une image massive qui a la particularité d'indiquer un sens qui la déborde par sa fonction technique mais aussi par la sollicitation qu'elle exerce sur le système visuel d'Homo en raison de sa forme : par dessus les mains manipulatrices, le regard indexateur et indicialisant d'Homo y va vers la pointe.

Ensuite, sur les parois peintes du paléolithique, où elle apparaît comme image détaillée, la flèche est un trait-point complété d'une indication de sens par quelques autres traits-points obliques situés à son extrémité ou sur son corps. Là, à nouveau, l'indication temporelle d'un mouvement directionnel est obtenue par une polarisation du système visuel et par l'évocation d'une fonction technique, le percement. La charge rituelle, chasseresse ou sexuelle, est considérable.

En effet, avec son mouvement implicite, la flèche signe va d'un "ici" à un "là", lequel tantôt est particulier, comme un point d'arrivée concret, tantôt est général, comme un ailleurs. Dans les deux cas, elle déclenche un double effet de champ perceptivo-moteur rudimentaire. Car sa gravitation propre d'image visuelle y est ouverte (étirée), d'une part en raison de celle de l'attracteur "là", d'autre part en raison du mouvement corporel qu'elle induit du fait de son but visé, du fait aussi qu'elle est perçue comme ayant résulté d'un mouvement dirigé vers ce but physique ou mental, et qui fait qu'elle est le signe de piste par excellence.

* * *

Faisant suite au triangle des forces de Stevin (1586), dont descendra le parallélogramme des forces, la flèche image, dans la mathématique du XIXe siècle, a d'abord eu un statut géométrique. Comme il convenait à sa nature conductrice, c'est un vecteur (vehere, conduire en tirant), c'est-à-dire un segment comportant une origine et une extrémité qui ne sont pas interchangeables, et qui donc produisent un sens et une direction. Cependant, par exemple chez Chasles, les segments vectoralisés donnent lieu à une sorte d'algèbre (calcul) géométrique orientée. Et du coup l'apparition de la flèche nulle, forcée par l'algèbre, trahit qu'on est en train de sortir de la simple image.

Et en effet, avec l'élaboration ultérieure du calcul vectoriel, la flèche développe considérablement ses possibilités d'évocation, ou plutôt de désignation. Grâce à son sens et à sa longueur, la voici en état de représenter toutes les grandeurs intensives : vitesses, forces orientées. Par quoi se faisait jour une première géométrisation de la cinématique, voire de la dynamique du point.

Bien plus, ce premier glissement conceptuel accompli, on ne s'étonnera pas que la flèche ait écrit l'opération logique de l'implication, "si...alors", laquelle part d'un antécédent et aboutit à un conséquent. Cette fois elle perdait son statut géométrique : sa longueur n'importait plus, seule subsistait l'indication d'un point de départ et d'un point d'arrivée non situés spatialement et purement conceptuels. Avaient lieu une déspatialisation physique, puisqu'il ne s'agit plus d'étendue, et la création d'une sorte de spatialisation conceptuelle dans une écriture pure. Ceci évoque le titre de Frege de 1879 : Begriffschrift (écriture du concept).

* * *

On assista alors à une vraie révolution graphique : la flèche pour désigner la fonction. Etant donnés deux ensembles quelconques A et B, une fonction de A vers B est une correspondance qui à chaque élément a de l'ensemble A associe un élément b bien déterminé de l'ensemble B, élément que depuis Leibniz on note : f(a). L'invention d'écriture fut d'écrire :

Dans l'histoire de l'écriture mathématique, il n'y a eu que deux autres inventions de pareille importance. La première, antique, tint dans la mise en usage de lettres pour désigner des objets mathématiques. La deuxième, essentiellement à la Renaissance, tint en de nouveaux signes abréviateurs : = , +, etc. La flèche désignatrice de fonction permettra une écriture bidimensionelle ou même tridimensionnelle. En effet, si

 et 

sont deux fonctions, on peut les composer en la fonction g ¡ f, laquelle à chaque élément a de A associe l'élément c de C déterminé par c = g(f(a)).

On peut alors donner sens à une phrase comme : Le carré

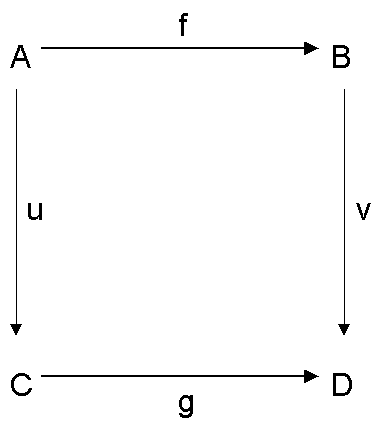
commute. C'est simplement v ¡ f = g ¡ u

Et on peut du même coup écrire aussi une phrase comme : Si le cube

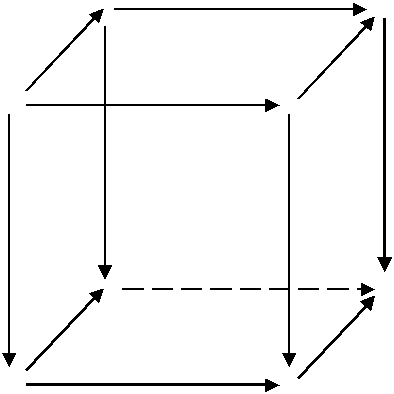
commute, et si toutes ses faces autres que la face supérieure ont la propriété P, alors la face supérieure a aussi la propriété P.

Quel est en l'occurence le statut du cube dessiné? Celui d'une phrase écrite, et non d'un objet extérieur à la langue. En présence du carré syllogistique des scolastiques, ou des cercles d'Euler, ou des graphiques en général, on se trouvait en présence d'un mixte d'écriture et de dessin, croisant une désignation macrodigitale et une désignation analogique. Au contraire, notre dernier cube appartient vraiment à l'écriture.

Et cela moyennant un effet de champ logico-sémiotique. Car, d'une part, l'ordre du macrodigital devient ici pluridimensionnel, il s'ouvre sur l'espace à l'intérieur de lui-même ; le cube dessiné est bien une phrase écrite. Mais, d'autre part, ce cube ne cesse pas pour autant d'être un dessin, une analogie de cube, avec ses faces et ses arrêtes.

* * *

Sans doute commençe-t-on là à pénétrer dans le MONDE 3 de l'écriture. Mais, pour y accéder pleinement, une étape restait à franchir. C'était d'abstraire la flèche de sa contiguïté avec la notion de fonction dans ce qu'elle comportait encore d'adhérence à la fonction concrète.

La nouvelle possibilisation a été de considérer que la flèche pouvait inscrire toute transformation adaptée à une situation mathématique définie. Lorsqu'un mathématicien s'intéresse à une structure donnée, il ne vise pas seulement la classe des objets munis de cette structure, mais aussi la classe des transformations adaptées à cette structure. Ainsi les topologues ne s'intéressent pas seulement aux espaces topologiques, mais aussi, et peut-être surtout, aux fonctions continues. Les opérateurs linéaires sont plus importants pour les algébristes que les espaces vectoriels. Les représentations, ou homomorphismes, de groupes sont au moins aussi fondamentaux que les groupes eux-mêmes. Et chacune de ces transformations, dans le contexte (la circonstance) d'une situation mathématique donnée, peut s'écrire comme une flèche.

On s'aperçoit alors que les classes de ces flèches, - classe des fonctions, classe des fonctions continues, classe des homomorphismes, classe des fonctions différenciables, etc., - ont elles-mêmes une structure algébrique originale. Dans chacune, la composée de deux flèches existe et est une flèche du même type. Dans chacune aussi, chaque objet est porteur d'une flèche "insignifiante", la flèche identité, c'est-à-dire la transformation qui consiste à laisser tout en place.

Pour leur composition, leur source, leur but, leur flèche identité, la structure de ces ensembles de flèches devient une structure algébrique comme les autres. C'est ce qui, par une audace philosophique peu banale, due à S. Eilenberg et S. Mac Lane, a été nommé une catégorie. Le mot est très fort puisqu'il rattache ce thème mathématique fondamental à ce qu'Aristote avait appelé les catégories (aï katègoriaï) pour désigner épistémologiquement les différentes classes des prédicats qu'on peut attribuer dans un jugement à un sujet quelconque, grammatical ou réel ; et donc ontologiquement les différentes classes de l'être.

* * *

Mais, même dans une catégorie, on continue à noter des flèches par des flèches, et à dire que le carré déjà rencontré

commute, c'est-à-dire que v ¡ f = g ¡ u, puisque les flèches se composent sans qu'on sache ce qu'elles "sont", si ce n'est des éléments composables d'une catégorie définie par ses axiomes.

Or ceci ouvre des perspectives très étranges, qu'on rencontre souvent dans la mathématique d'aujourd'hui. Je me contenterai d'un exemple montrant que l'on peut en arriver à dire qu'un concept est l'image en miroir d'un autre, et que cela fait sens. Ainsi appelle-t-on produit de deux objets A et B un objet P muni de deux flèches, u de P vers A et v de P vers B, tel que pour tout objet X muni également de deux flèches, f de X vers A et g de X vers B, il existe une et une seule flèche de X vers P faisant commuter le diagramme :

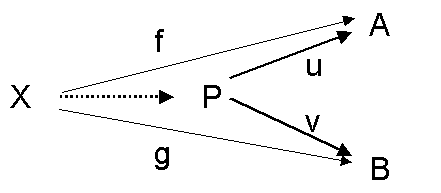
L'image en miroir de ce concept de produit est ce que l'on appelle une somme de deux objets A et B. C'est un objet Q muni de deux flèches u de A vers Q et v de B vers Q tel que pour tout autre objet X muni également de deux flèches, f de A vers X et g de B vers X, il existe une et une seule flèche de Q vers X faisant commuter le diagramme :

Il n'est pas nécessaire de savoir ce que pourraient bien être ces objets P et Q pour voir que ces concepts de produit et de somme sont reliés par une propriété purement graphique, purement scripturale, de retournement du sens des flèches. Nous avons donc ici un lieu, dans la mathématique même, où ce n'est pas simplement l'espace qui se mue en signe, mais le signe qui se mue en espace, de par la spatialité même de son écriture. On se trouve en un point d'interférence entre l'espace et la logique.

Henri Van Lier, 25 juin 1995

* * *

On pourrait faire un pas de plus dans cette direction. La flèche ne pourrait-elle pas subvertir la logique et jusqu'au concept d'ensemble?

Car, au niveau le plus élémentaire, la logique a un rapport avec le concept général d'ensemble. L'ensemble des parties P(M) d'un ensemble M est muni d'opérations (l'intersection, la réunion, le complémentaire) qui évoquent clairement les connecteurs logiques classique (la conjonction ∧ , la disjonction ∨ , la négation ¬ ). Pour faire varier la logique, comme nous le suggère la flèche, il faut donc commencer par faire varier le concept même d'ensemble, ce qui conduit aux notions de faisceau et de topos.

Un topos est essentiellement une catégorie E (au sens défini plus haut) qui, outre quelques conditions élémentaires, permet d'associer à chacun de ses objets X un objet P(X), objet des parties de X, jouant à l'intérieur de E le rôle que joue l'ensemble des parties d'un ensemble dans le cas usuel des ensembles. Pour être un peu plus précis, prenons deux objets X et Y de E. Considérons l'ensemble des relations de Y vers X, c'est-à-dire l'ensemble des sous-objets du produit Y x X (au sens du mot produit que nous venons de décrire). Si nous étions dans les ensembles, une relation de Y vers X serait simplement un ensemble de couples (y,x) d'éléments de Y et X, tandis qu'ici il faut dire que c'est un certain sous-objet de l'objet Y x X. La condition sur l'objet P(X) est alors que l'ensemble des relations de Y vers X soit en bijection, de manière naturelle, avec l'ensemble des flèches de E allant de l'objet Y vers l'objet P(X).

Pour suggérer l'intérêt philosophique et donc anthropologique de ce concept de topos, considérons l'exemple simple des ensembles variants à deux états. Se donner un tel ensemble variant X c'est se donner ce qu'il était avant, disons X₀, se donner ce qu'il sera après, disons X₁, mais surtout se donner une fonction f indiquant pour chaque élément de X₀ ce qu'il deviendra après dans X₁ ; autrement dit, f indique pour chaque x₀ de X₀ quel sera f(x₀) dans X₁. L'ensemble variant X, ou l'objet X de la catégorie des ensembles variants à deux états, est le triple (f, X₀, X₁) et on écrira X = (f : X₀ → X₁). C'est un peu alors comme si le changement intervenait au niveau même du concept d'ensemble. Un ensemble variant est globalement f : X₀ → X₁. Tout est décrit comme si les ensembles variaient avec un temps simplifié du type 0 → 1, c'est-à-dire un avant, un après, un unique changement, bref une unique transformation.

Dans cette situation très simplifiée, on a à la base la flèche comme un réel, ou comme un temps à deux états. Et on a, au-dessus de cette base, comme une superstructure tout un univers variant avec ses objets (ses ensembles) mais aussi sa logique et sa vérité. Par exemple, dans les ensembles classiques il y a un ensemble de valeurs de vérités Ω = {0,1} qui ne contient que deux éléments : le vrai, noté 1, et le faux, noté 0. On peut voir que pour les ensembles variants, - autrement dit dans le topos des ensembles variants, - il y a un ensemble variant de valeurs de vérité

Autrement dit, ce qui était vrai restera vrai, ce qui était faux restera faux, et ce qui était "?" deviendra vrai. Dans une sorte d'ailleurs absolu par rapport au temps et à l'univers qu'est en somme l'imaginaire du mathématicien, on pourrait donc dire que "?" correspond à la "valeur de vérité" : "cela ne se savait pas encore, mais cela deviendra vrai".

Cet exemple donne une petite idée de ce que peut être un topos. Mais, la base ne comportant qu'une seule flèche, il est simpliste. Il faudrait considérer un "temps" plus complexe, telle une base formée d'un "temps bifurquant" comme celui du schéma ternaire :

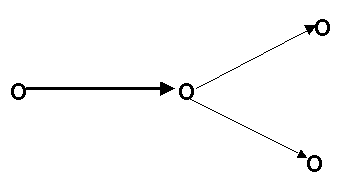
Ou un temps représenté par un ensemble ordonné quelconque. On peut aussi accepter diverses transitions entre les "instants" de ce temps généralisé et considérer, entre autres, un "temps" généralisé à seulement deux états mais à deux transitions :

Et dire même que la base peut être une catégorie quelconque. Ou finalement, en un sens qui serait à préciser, que la base est un "espace" ou un "site" quelconque.

C'est ce cas spatial qui fut au départ de la notion de topos telle que A. Grothendieck l'introduisit en 1960 pour les besoins de la géométrie algébrique. En 1965, F.W. Lawvere définissait son extension logique, et notamment le rôle privilégié de l'objet Oméga des valeurs de vérité. L'étymologie est riche de sens : le topos grec était un lieu animé par un événement : l'endroit qu'on foule, qu'on occupe, qui est le siège d'un mal, qui donne accès à. Du coup, dès Isocrate et Eschine, topos désigna le fondement d'un raisonnement quelconque, jusqu'au koinos topos, d'où vient notre "lieu commun".

Destin exemplaire que celui de la flèche, qui d'objet-outil passe à l'image massive, puis devient comme le paradigme de l'index. Elle déclenche un champ perceptivo-moteur, puis logico-sémiotique, pour constituer aujourd'hui, dans le MONDE 3, la base de tout système.